24. Arrays, II¶
In this section, we will assume we did first import numpy using
its standard abbreviation np:
import numpy as np
24.1. Index notation¶
The index notation from translating mathematical vectors to arrays
carries directly to translating matrices. In computing, these are
just referred to as multidimensional arrays, or more commonly just
"arrays" (in actual fact, a multidimensional array is just an array
whose elements are also arrays, an "array of arrays", but that
normally is not relevant when using them). All the above notations and
terms apply. Matrices typically have multiple dimensions and
therefore multiple indices; these also translate directly from
subscripts in the mathematics to square brackets in computing. For
example, the element in the first row and column of a 2-dimensional
matrix would be
A[0, 0]; the next element in
the column would be A[1, 0]; etc.
24.2. Creating arrays with known values¶
In the previous sections, we have introduced various numpy
functions for easily creating special types of vectors/matrices:
np.zeros((3,4))
array([[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
np.ones((2,3))
array([[ 1., 1., 1.],
[ 1., 1., 1.]])
v3 = np.arange(10) #Output: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
v4 = np.linspace(-2, 2, 5) #Output: array([-2., -1., 0., 1., 2.])
We have also introduced list comprehensions and it is important to note that an array can be created by simply sending the resulting list to the array constructor:
squares = np.array([n**n for n in range(6)])
print(squares)
array([[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
array([ 0, 1, 4, 9, 16, 25])
Python offers more functions to create arrays. np.full Creates an array of the given shape initialized with the given value. Here's a 2x3 array full of π.
np.full((2,3), np.pi)
array([[ 3.14159265, 3.14159265, 3.14159265],
[ 3.14159265, 3.14159265, 3.14159265]])
24.3. Creating arrays with random values¶
Sometimes, we need to create arrays initialized with random values. Many functions are available in NumPy's random module to create such arrays. We'll start by defining three random arrays, a one-dimensional, two-dimensional, and three-dimensional array.
a1 = np.random.randint(20, size=6) # One-dimensional array
a2 = np.random.randint(20, size=(3, 4)) # Two-dimensional array
a3 = np.random.randint(20, size=(3, 4, 5)) # Three-dimensional array
Run these lines several times and look at the resulting arrays. You will realize that each time you run the code, different values are generated. In order to ensure that the same random arrays are generated each time this code is run, we'll use NumPy's random number generator, which we will seed with a set value before the random arrays creation :
np.random.seed(0) # seed for reproducibility
Furthermore, it is possible to create a random array by sampling from a specific distribution. For example, here is a 3x4 array initialized with random floats between 0 and 1 (uniform distribution):
np.random.rand(3,4)
array([[ 0.15802446, 0.43477402, 0.81614133, 0.62811013],
[ 0.57390644, 0.69407189, 0.89299862, 0.58584783],
[ 0.25014968, 0.10522317, 0.36393147, 0.72826021]])
Here's a 3x4 array containing random floats sampled from a univariate normal distribution (Gaussian distribution) of mean 0 and variance 1:
np.random.randn(3,4)
array([[-0.37698199, -0.71092541, 0.77823299, 1.8110648 ],
[ 0.1160549 , -0.21966641, -0.31370215, -0.33533435],
[ 1.38330925, 0.29539509, 0.28905152, 0.1313947 ]])
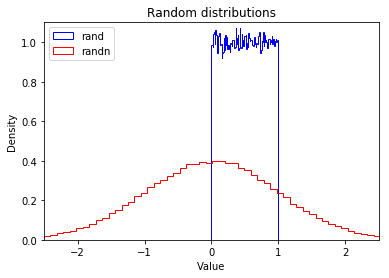
To give you a feel of what these distributions look like, let's use the matplotlib module:
import matplotlib.pyplot as plt
plt.hist(np.random.rand(100000), normed=True, bins=100, histtype="step", color="blue", label="rand")
plt.hist(np.random.randn(100000), normed=True, bins=100, histtype="step", color="red", label="randn")
plt.axis([-2.5, 2.5, 0, 1.1])
plt.legend(loc = "upper left")
plt.title("Random distributions")
plt.xlabel("Value")
plt.ylabel("Density")
plt.show()
24.4. Attributes of arrays¶
Each array has attributes ndim (the number of dimensions), shape
(the size of each dimension), and size (the total size of the
array):
np.random.seed(0)
a = np.random.randint(10, size=(4, 3))
print("a: ", a)
print("a ndim: ", a.ndim)
print("a shape:", a.shape)
print("a size: ", a.size)
a: [[5 0 3]
[3 7 9]
[3 5 2]
[4 7 6]]
a ndim: 2
a shape: (4, 3)
a size: 12
Another useful attribute is the dtype, the data type of the array
(which we discussed previously in Arrays, I: Creating arrays):
print("dtype:", a.dtype)
dtype: int64
24.5. Accessing single elements¶
In a one-dimensional array, a single element is accessed by its index as discussed in the section Arrays, I. In a multi-dimensional array, items can be accessed using a comma-separated sequence of indices:
np.random.seed(0)
a = np.random.randint(10, size=(4, 3))
array([[5 0 3],
[3 7 9],
[3 5 2],
[4 7 6]])
a[0, 0]
5
a[2, 0]
3
a[2, -1]
2
Values can also be modified using any of the above index notation:
a[0, 0] = 8
array([[8 0 3],
[3 7 9],
[3 5 2],
[4 7 6]])
Keep in mind that, NumPy arrays have a fixed type. This means, for example, that if you attempt to insert a floating-point value into an integer array, the value will be silently converted.
a[1,2] = 4.2 # this will be converted to integer!
array([[8, 0, 3],
[3, 7, 4],
[3, 5, 2],
[4, 7, 6]])
24.6. Slicing of arrays¶
Multi-dimensional slices work in the same way as one-dimensional arrays (introduced in Arrays, I), with multiple slices separated by commas. For example:
np.random.seed(1)
x = np.random.randint(10, size=(3, 4))
array([[5, 8, 9, 5],
[0, 0, 1, 7],
[6, 9, 2, 4]])
x[:2, :3] # two rows, three columns
array([[5, 8, 9],
[0, 0, 1]])
x[:3, ::2] # all rows, every other column
array([[5, 9],
[0, 1],
[6, 2]])
One commonly needed routine is accessing of single rows or columns of an
array. This can be done by combining indexing and slicing, using an
empty slice marked by a single colon (:):
print(x[:, 0]) # first column of x
[5, 0, 6]
print(x[0, :]) # first row of x
[5, 8, 9, 5]
In the case of row access, the empty slice can be omitted for a more compact syntax:
print(x[0]) # equivalent to x[0, :]
One extremely important and useful thing to know about array slices is that they return views rather than copies of the array data. To better illustrte this, let us consider our two-dimensional array from before:
print(x)
[[5 8 9 5]
[0 0 1 7]
[6 9 2 4]]
Let's extract a subarray from this:
x_subar = x[:2, :2]
print(x_subar)
[[5 8]
[0 0]]
Now if we modify this subarray, we'll see that the original array is changed! Observe:
x_subar[1, 0] = 57
print(x_subar)
[[5 8]
[57 0]]
print(x)
[[ 5, 8, 9, 5],
[57, 0, 1, 7],
[ 6, 9, 2, 4]]
This default behavior is actually quite useful: it means that when we work with large datasets, we can access and process pieces of these datasets without the need to copy the underlying data buffer.
Nevertheless, it is sometimes useful to instead explicitly copy the data of interest to a new array to be able to modify the copy without affecting the original. This can
be most easily done with the copy() method:
x_subar_copy = x[:2, :2].copy()
print(x_subar_copy)
[[5 8]
[0 0]]
If we now modify this subarray, the original array is not affected:
x_subar_copy[1, 0] = 42
print(x_subar_copy)
[[ 5 8]
[42 0]]
print(x)
[[5 8 9 5]
[0 0 1 7]
[6 9 2 4]]
24.7. Reshaping of arrays¶
Another useful type of operation is reshaping of arrays. The most
flexible way of doing this is with the reshape method. For example,
if you want to put the numbers 1 through 16 in a grid,
you can do the following:
grid = np.arange(1, 17).reshape((4, 4))
print(grid)
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]
[13 14 15 16]]
Note that for this to work, the size of the initial array must match the size of the reshaped array. Another common reshaping pattern is the conversion of a one-dimensional array into a two-dimensional row or column matrix.
x = np.array([1, 2, 3])
# row vector via reshape
x.reshape((1, 3))
array([[1, 2, 3]])
# column vector via reshape
x.reshape((3, 1))
array([[1],
[2],
[3]])
Actually, we can reshape into any shape, as long as the elements required for reshaping are equal in both shapes.
24.8. Concatenation and splitting of arrays¶
All of the preceding routines worked on single arrays. It's also possible to combine multiple arrays into one, and to conversely split a single array into multiple arrays. We'll take a look at those operations here.
24.8.1. Concatenation of arrays¶
Concatenation, or joining of two arrays in NumPy, is primarily
accomplished using the routines np.concatenate, np.vstack, and
np.hstack. np.concatenate takes a tuple or list of arrays as its
first argument, as we can see here:
x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
np.concatenate([x, y])
array([1, 2, 3, 4, 5, 6])
You can also concatenate more than two arrays at once:
z = [7, 8, 9]
print(np.concatenate([x, y, z]))
[1 2 3 4 5 6 7 8 9]
It can also be used for two-dimensional arrays:
grid1 = np.array([[1, 2, 3],
[4, 5, 6]])
grid2 = np.array([[ 7, 8, 9],
[10, 11, 12]])
# concatenate along the first axis
np.concatenate([grid1, grid2])
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
# concatenate along the second axis (zero-indexed)
np.concatenate([grid1, grid2], axis=1)
array([[ 1, 2, 3, 7, 8, 9],
[ 4, 5, 6, 10, 11, 12]])
For working with arrays of mixed dimensions, it can be clearer to use
the np.vstack (vertical stack) and np.hstack (horizontal stack)
functions:
x = np.array([1, 2, 3])
grid = np.array([[4, 5, 6],
[7, 8, 9]])
# vertically stack the arrays
np.vstack([x, grid])
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# horizontally stack the arrays
y = np.array([[99],
[100]])
np.hstack([grid, y])
array([[ 4, 5, 6, 99],
[ 7, 8, 9, 100]])
Similarly, np.dstack will stack arrays along the third axis.
24.8.2. Splitting of arrays¶
The opposite of concatenation is splitting, which is implemented by the
functions np.split, np.hsplit, and np.vsplit. For each of
these, we can pass a list of indices giving the split points:
x = [5, 8, 9, 4, 3, 0, 1, 7, 6, 10]
x1, x2, x3 = np.split(x, [3, 5])
print(x1, x2, x3)
[5 8 9] [4 3] [ 0 1 7 6 10]
Notice that N split-points, leads to N + 1 subarrays. The related
functions np.hsplit and np.vsplit are similar:
grid = np.arange(16).reshape((4, 4))
grid
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
upper, lower = np.vsplit(grid, [2])
print(upper)
print(lower)
[[0 1 2 3]
[4 5 6 7]]
[[ 8 9 10 11]
[12 13 14 15]]
left, right = np.hsplit(grid, [2])
print(left)
print(right)
[[ 0 1]
[ 4 5]
[ 8 9]
[12 13]]
[[ 2 3]
[ 6 7]
[10 11]
[14 15]]
Similarly, np.dsplit will split arrays along the third axis.