15. Plotting, I: View 1D array(s)¶

We often want to visualize data or results. There are many, many ways to make graphs, plots or images, depending on the type of data and context. We start here by considering basic plotting of two variables, i.e., the classic "x-y" plots.

We will meet Python's Matplotlib module, which will be essential to this work. Additionally, we will also use the NumPy module quite a bit, because we will be working with arrays:

import matplotlib.pyplot as plt     # for plotting
import numpy as np                  # for working with arrays

15.1. Basic plot ¶

Let's say we're interested in plotting a relation between two variables such as $y = x^2$ in a given interval $x \in [-2, 2].$ Mathematically, there is a continuous relationship between two real numbers, and that all the values are well-behaved (no infinities). How do we use a computer to display this?

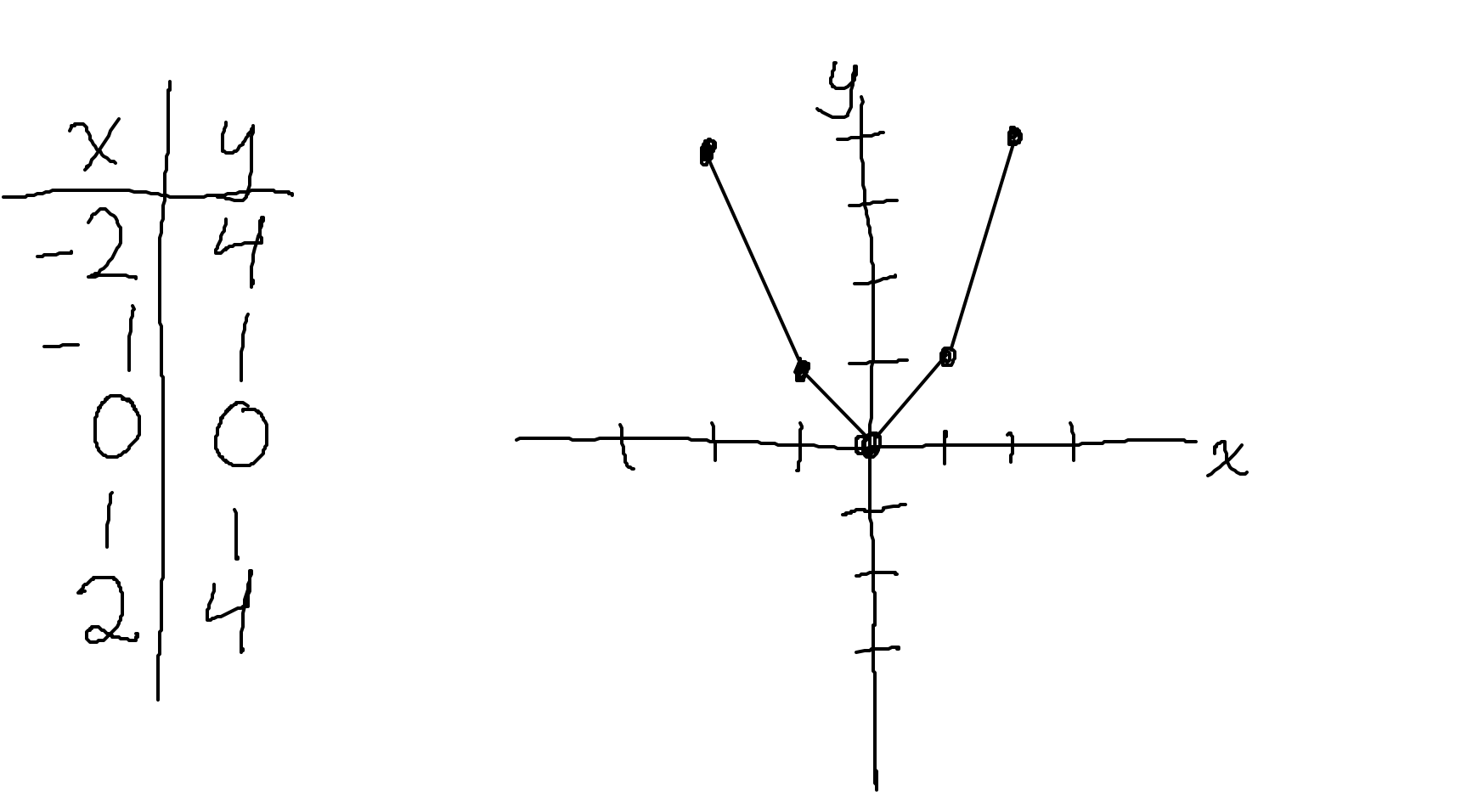
Well, Python will not be able to generate a plot of $x$ and $y$ from the abstract/generalized mathematical formula above. We will need to generate concrete values to approximate the curve and then plot these. Essentially, we have to back to basics, to our early school days when we learned to plot by hand. To approximate a continuous curve, we: made a column of $x$ values and then a corresponding column of calculated $y$ values; drew a coordinate plane and placed a dot on it for each $(x_i, y_i)$ pair; and then connected the dots in order using a straight line segment. Below is the kind of image that would result, and in fact this is exactly how we will harness the amazing technological innovations of computers:


Recalling early days of simple plotting: construct two columns of numbers, with each ith row providing an $(x_i, y_i)$ pair to be placed on the graph at the right. The pairs can be connected by straight lines for (sometimes blocky) continuity.

In the previous section, we studied 1D arrays. Do you see any way we can apply knowledge here? Well, looking at the sequence of numbers in x and y above, each looks like a 1D array, doesn't it? Indeed, to start translating what the above into programming, we can first use arrays to store the values of the x and y columns. We might notice that x has evenly spaced values, so we could use a numpy function built for making such an array easily; for y, we will just type out the values:

x = np.linspace(-2, 2, 5)            # 5 values: -2. -1.  0.  1.  2.
y = np.array([4, 1, 0, 1, 4])

Looking at our plot above, we should appreciate that the x and y arrays must always have the same length: each point is a coordinate pair of a corresponding element in the two arrays---e.g., $(x_0, y_0)$ or, programmatically, (x[0], y[0]).

Q: How could you write a Python expression to check that the two arrays have the same length?

+ show/hide code

We can then make use of the plt.plot() function to generate the graph of the element pairs. Let's look at its help for usage via plt.plot?. Here, we just show the top section of the docstring (which is quite long, with a great amount of control of plotting behavior) and then the top part of the description of the parameters (which is further down in the help):

Signature: plt.plot(*args, scalex=True, scaley=True, data=None, **kwargs)
Docstring:
Plot y versus x as lines and/or markers.

Call signatures::

    plot([x], y, [fmt], *, data=None, **kwargs)
    plot([x], y, [fmt], [x2], y2, [fmt2], ..., **kwargs)

The coordinates of the points or line nodes are given by *x*, *y*.

The optional parameter *fmt* is a convenient way for defining basic
formatting like color, marker and linestyle. It's a shortcut string
notation described in the *Notes* section below.

>>> plot(x, y)        # plot x and y using default line style and color
>>> plot(x, y, 'bo')  # plot x and y using blue circle markers
>>> plot(y)           # plot y using x as index array 0..N-1
>>> plot(y, 'r+')     # ditto, but with red plusses

...

Parameters
----------
x, y : array-like or scalar
    The horizontal / vertical coordinates of the data points.
    *x* values are optional and default to `range(len(y))`.

    Commonly, these parameters are 1D arrays.

In Line 1, we see a couple keyword args provided, but in fact there are too many possible input parameters and combinations to list there individually, so the help just puts *args and **kwargs to denote that more of each kind of input are possible. Looking at the example call signatures in Lines 7-8, we see thing that might be what we want we want: plotting one or two 1D arrays (because in lines 25-27, we see that that is what x and y commonly represent). In Lines 16-17 we see basic examples of plotting "y vs x", or in Lines 18-19 we see we could just "y" by itself, with abscissa values automatically made as int values from $[0, N)$ . These look usable with the arrays we have, so let's try the first one from Line 16:

plot(x, y)
plt.show()

Why are there two commands needed here? Well, plotting is generally is a two-step process in Python: first, make the plot; then, show the plot. And that plot looks like this:

... which is basically what we had above (just without the $x=0$ and $y=0$ lines). What do the other three example plots in Lines 17-19 look like? They play around with plotting styles and properties. For example, they show the points separately with "marker" symbols and change colors: 'bo' is a shortcut, where "b" is for blue and "o" for a circle marker; 'r+' is similar, but for red cross markers. By putting only one array in the positional arguments, the x-axis becomes the integer-spaced values from $[0, N)$ :


`plt.plot(x,y, 'bo')`	`plt.plot(y)`	`plt.plot(y, 'r+')`

Note that the cases of only y being plotted are not appropriate here; the curve is effectively shifted to the right, as seen by the minimum appearing where x=2. But in other cases, it might be a useful syntax.

There is a lot of overlapping functionality across Matplotlib functions and arguments to control the appearance of plots. We will try to introduce a starting sampler of optionality, below. In all cases, we recommend browsing the help docstrings of the mentioned functions, as well as explore others in the module.

15.2. Plot styles and properties ¶

More than one line can be plotted on a graph. Let's add another array of ordinates (and keep the same x-values):

y2 = np.array([-1, 2, 0.5, -0.5, 1])

By default, Python will add new lines with distinct colors, but let's look at specifying colors, as well as line styles and marker styles. In most cases we will specify these things with keyword arguments to the plotting function.

Again, the plt.plot? doc string is long, but under "Properties:" there is a list of kwargs, of which a few relevant ones are:

...
Properties:
color or c: color
linestyle or ls: {'-', '--', '-.', ':', '', (offset, on-off-seq), ...}
linewidth or lw: float
marker: marker style
markeredgecolor or mec: color
markeredgewidth or mew: float
markerfacecolor or mfc: color
markerfacecoloralt or mfcalt: color
markersize or ms: float
...

In some cases there is both a long and short version of the same keyword (e.g., linewidth and lw). To the right of the colon, the kind of expected value is listed, in most cases here either a float (for a size) or a string (for a color or style). Example linestyle values are provided there, but in many few cases of interest the list is so long that they are displayed further down in the doc string; we provide a few here:

+ show/hide plot markers
+ show/hide plot line styles
+ show/hide plot color abbrevs

The basic plotting examples above showed how the character color abbreviations can be combined with either markers or line styles. And a gallery of Matplotlib's "named" colors is provided at the bottom of this page.

How do we use these parameters? Here is an example, showing two curves in a single figure:

plt.plot(x, y, color = 'magenta', ls = '-.', lw = 2, marker = 'v', ms = 8)

plt.plot(x, y2,
         color  = 'k',
         ls     = ':',
         lw     = 2,
         marker = 'o',
         mew    = 2,
         mec    = 'dodgerblue',
         mfc    = 'limegreen',
         ms     = 6)

plt.ion()
plt.show()

Some comments on these commands:

You can check the the descriptions of the keywords with the function's doc string or tables above.
We could have used some of the above abbreviations for color and lines, like m-. in place of color = 'magenta', ls = '-.', but once we are specifying a lot of options, using the full option names may be easier to read.
Note how in the second plt.plot command, we were specifying so many options that we decided to space them onto separate lines. This can be convenient for clarity, both for reading and changing options; the indentation of each option is not necessary here, it is a programming style choice that aids reading (as does vertically aligning the = symbols).
Calling the plt.ion() function just before plt.show() turns interactive mode "on", which will not add functionality in the Jupyter notebook environment, but if working in iPython allows one can keep typing commands without having to close the plot.
Plotted arrays are displayed in the order listed, so the first one will be furthest in the background and the last one in the foreground.

Anyways, the above leads to the colorful plot:

Note

Earlier, we noted that the Python interpreter reads each line separately, and if you want to spread a single command onto the next line you would use the continuation of line character \. How, then, can the above plt.plot() span Lines 3-11 without using \ at all?

It happens because there is an opening parenthesis ( in Line 3, and the interpreter will continue to treat everything it reads as part of that single expression until it reaches the closing ). See here for more examples of Python's automatic line continuation.

15.3. Titles, labels and axis details ¶

We can add a lot more features to the plot that really make it useful for presenting information. For example, right now we don't know anything about what the units along the x- and y-axes, and adding a title would be helpful to know what is being plotted.

We can even put a legend into the plot to show labels for each plot: this is done by adding a label = `` kwarg to each plot with a string value to display, and then use of the ``plt.legend() function before showing the plot. We can let Matplotlib guess a good location for the legend or specify it ourselves. Consider the following:

plt.plot(x, y, color = 'magenta', ls = '-.', lw = 2, marker = 'v', ms = 8,
         label = 'y')

plt.plot(x, y2,
         color  = 'k',
         ls     = ':',
         lw     = 2,
         marker = 'o',
         mew    = 2,
         mec    = 'dodgerblue',
         mfc    = 'limegreen',
         ms     = 6,
         label  = 'y2')

plt.xlabel('x (in meters)')
plt.ylabel('data measurement (in meters)')
plt.title('Important results')
plt.legend(loc='upper center')

plt.ion()
plt.show()

Note

Python can interpret LaTeX's "math mode" in strings. So if you are familiar with this powerful way to write technical expressions, you can spice up your plots. Just note that LaTeX's escape character \ is also recognized as such in Python, and so one has to include 2 of them in most cases so that it gets passed through to LaTex correctly.

For example, we could use the formula $y \approx x^2$ in the first plot's label, above. In pure Latex, this would be encoded as $y \approx x^2$ ; however, the Python string in the label would have to contain it as: $y \\approx x^2$ . You can verify this in the string label above.

Matplotlib estimates default ranges of both the x- and y-axes to display the full area of plotted points. The limits of each can be set separately with plt.xlim() and plt.ylim() functions, respectively. (Here and below, if there is a plt.xSOMETHING() function, one can generally expect to find a plt.ySOMETING() function with similar parameters and syntax, and vice versa.) Note that setting the bounds this way can chop of pieces of the plot.

Additionally, we can set the relative units or ratio of units between the two axes. For example, if the axes both share the same units, we might want to make sure that a distance between the "0" and "1" in each case covers the same amount of plot space; that is, a circle should appear as a circle, not as an oval because one axis is stretched compared to another (by default, the module will not try to ensure this -- it treats the axis units as independent). The plt.axis() function can take the arguments 'scaled' and 'equal' as two different ways to try to enforce the relationship of axis units: the former tries to adjust the dimensions of the plot, and the latter tries to change the ranges (so it might lead to ignoring plt.xlim and plt.ylim settings).

The locations along the plot edges with dashes and numbers labelling the axis are known as major ticks. Matplotlib has some inner formula to place these by default. But you can pass an array of values for the tick locations along either axis with plt.xticks() or plt.yticks(). The ticks can even be turned off by passing an empty list with, for example, plt.xticks([])

The axes are labelled with numbers, but sometimes adding in the standard x- and y- axes provide useful visual cues. While we could make more arrays to accomplish this, there are Matplotlib functions for plotting such lines: plt.axhline() plots a horizontal line that is by default at $y=0$ and across the entire plot; and plt.axvline() is the vertical analogue. If we might want these to be in the background, we would plot these before the main curves. As a style point, I often like making these light gray (instead of default black) and a bit thinner than the default.

As we start making several plots, it can be useful to use the plt.figure() function to signify the start of a new plot; otherwise, we might just keep adding to existing plots accidentally. Later, we will also see that we can control useful feature about the plot (size, dimensions, resolution) using this function, too.

plt.figure("example plot 7")

plt.axhline(c = '0.75', lw = 0.5)  # horiz line (def, y=0), light gray color
plt.axvline(c = '0.75', lw = 0.5)  # vert line (def, x=0), light gray color

plt.plot(x, y, color = 'magenta', ls = '-.', lw = 2, marker = 'v', ms = 8,
         label = 'y')

plt.plot(x, y2,
         color  = 'k',
         ls     = ':',
         lw     = 2,
         marker = 'o',
         mew    = 2,
         mec    = 'dodgerblue',
         mfc    = 'limegreen',
         ms     = 6,
         label  = 'y2')

plt.axis('scaled')             # call *before* plt.xlim and plt.ylim
plt.xlim(-3, 3)
plt.ylim(-1, 5)
plt.yticks(ticks=np.linspace(-1,5.5, 0.5))

plt.xlabel('x (in meters)')
plt.ylabel('data measurement (in meters)')
plt.title('Important results for the $^2\\Psi_\\alpha$ particle')
plt.legend()                   # let plt guess a good legend location

plt.ion()
plt.show()

... which leads to:

15.4. Grid of plots ¶

In addition to displaying several curves in the same plot, we can also make a single figure with several plots. There are multiple syntaxes for doing this. At its most basic, we can picture the figure being made up of an $N \times M$ matrix of plots, which we can walk through, row-by-row from the upper left plot (and each plot is indexed from $[1, NM]$ ), adding relevant details to each one. This is specified with plt.subplot(), which is used to indicate both the dimensions of the grid and which particular plot we want to edit. From its docstring plt.subplot?:

Signature: plt.subplot(*args, **kwargs)
Docstring:
Add a subplot to the current figure.

...

Call signatures::

   subplot(nrows, ncols, index, **kwargs)
   subplot(pos, **kwargs)

...

Parameters
----------
*args
    Either a 3-digit integer or three separate integers
    describing the position of the subplot. If the three
    integers are *nrows*, *ncols*, and *index* in order, the
    subplot will take the *index* position on a grid with *nrows*
    rows and *ncols* columns. *index* starts at 1 in the upper left
    corner and increases to the right.

    *pos* is a three digit integer, where the first digit is the
    number of rows, the second the number of columns, and the third
    the index of the subplot. i.e. fig.add_subplot(235) is the same as
    fig.add_subplot(2, 3, 5). Note that all integers must be less than
    10 for this form to work.

In the "Parameters" section, the first paragraph under *args refers to the syntax of Line 9. The second paragraph under there refers to Line 10. They both contain the same information: basically, if each of the number of rows, number of columns and total number of plots is a single digit ( $<10$ ), then you can use the "simpler" second form. Otherwise, you must use the first one. The descriptions above will probably be clearer with an example.

Let's first make another set of 1D arrays to plot:

x3 = np.array([-2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2])
y3 = np.array([4, 2.25, 1, 0.25, 0, 0.25, 1, 2.25, 4])

Where this is similar to the original x and y array pair, but with a smaller step size along the x-axis and hence a better approximation to the analytic $y=x^2$ curve. To see how this compares, we will plot this with the original 1D arrays on one subplot, and then put y2 on a second subplot.

plt.figure("subplot example")

plt.subplot(1, 2, 1)                  # first plot in 2x1 grid

plt.axhline(c = '0.75', lw = 0.5)
plt.axvline(c = '0.75', lw = 0.5)

plt.plot(x, y, label = 'step=1')
plt.plot(x3, y3, label  = 'step=0.5')

plt.axis('scaled')
plt.xlim([-2.5, 2.5])
plt.ylim([-2, 5])
plt.xlabel('x')
plt.ylabel('height')
plt.title('Approximations to $y=x^2$')
plt.legend()

plt.subplot(1, 2, 2)                  # second plot in 2x1 grid

plt.axhline(c = '0.75', lw = 0.5)
plt.axvline(c = '0.75', lw = 0.5)

plt.plot(x, y2, marker='o', c = 'green')

plt.axis('scaled')
plt.xlim([-2.5, 2.5])
plt.ylim([-2, 5])
plt.xlabel('x')
plt.title('The other plot')

plt.ion()
plt.show()

Since the number of plots is in single digits, we could have written the subplot commands in the abbreviated syntax: subplot(121) and subplot(122). In either case, the output plot would look the same:

15.5. Save to file ¶

Matplotlib contains a function to save a figure to a file, called plt.savefig(). You can use it instead of, or along with (e.g., calling it after), plt.show().

The main argument to provide is a positional one: the output filename. This filename can include path elements to write the file directly to another directory, otherwise it is written to the current working directory. The filename should typically include a relevant file extension, which is the short few characters at the end of a file (following ".") to specify the format of the file.

For images, png, jpg and tif are some the most common extensions or formats. These are all part of a grouping called rasterized images, for which you can think of the entire image being chopped up into a regular 2D grid to store the information; the lines and dots just paint in the grid elements to form the stored image. For such files, specifying the spatial resolution of the grid is important: just like with computer or cell phone screens, the images can be "nicer" and more detailed with higher resolution images. This is quantified with dots per inch (DPI), with greater DPI being higher resolution. Python uses some default DPI when saving images, but one can also specify kwarg in the function, such as:

plt.savefig("figure_01.png")                # save to current dir, def DPI
plt.savefig("../output_dir/figure_02.png")  # save to another dir, def DPI
plt.savefig("figure_03.png", dpi=300)       # save to current dir, set DPI

Having a higher DPI might produce a nicer image, or one that can be zoomed in usefully, but also a larger file size. How large the file size (and how it scales with DPI) depends on the image format; but that is precisely why there are different image formats: they store information differently, typically with an aim to compress the image into as small a size on the computer as possible. There is no universally "best" resolution -- the choice is usually context dependent. Many scientific journals require published figures to have a DPI of at least 300, but lower is probably fine for many applications.

A different class of images are known as vector graphics, which include svg, pdf (yes, the same one often used for text documents) and eps. These save the lines and letters of the plot as separate objects, which retain their identity when saved to file. This means that when zooming in, the image doesn't start looking grainy as the grid level gets reached. For line images and text, or images generated with lots of shapes, this can be a very useful file format. (If you have a standard photograph, then the continuous nature of most elements would rule out vector graphics as a good format.) Specifying a vector graphic file output follows the same syntax as for rasterized images, above:

plt.savefig("figure_01.svg")

etc.

Which file format is best for your image? You can always test a couple options and see-- be sure to check both the normal image, the zoomed image and the file size. There are also other file formats out there, too. Note that some have tradeoffs-- the above formats are all lossless meaning that they don't try to sacrifice image quality for file size, but other formats will (they are lossy). For example, gif is another rasterized graphic with fairly compact file size, but generally poor quality; it is popular for simple, lightweight web images and movies, but would not be a good choice for most plots.

Finally, we note if you want to control the size of the saved image, that is done using the figsize kwarg in the plt.figure() function. It is necessary to provide both the width and height of the final figure, so this pair of values must be grouped together, e.g.:

plt.figure("some fig label", figsize=(WIDTH, HEIGHT))

The units of WIDTH and HEIGHT are inches.

15. Plotting, I: View 1D array(s)¶

15.1. Basic plot ¶

15.2. Plot styles and properties ¶

15.3. Titles, labels and axis details ¶

15.4. Grid of plots ¶

15.5. Save to file ¶

Table of Contents

This Page

15. Plotting, I: View 1D array(s)¶

15.1. Basic plot¶

15.2. Plot styles and properties¶

15.3. Titles, labels and axis details¶

15.4. Grid of plots¶

15.5. Save to file¶

15.1. Basic plot ¶

15.2. Plot styles and properties ¶

15.3. Titles, labels and axis details ¶

15.4. Grid of plots ¶

15.5. Save to file ¶